Давайте представим себя в мире геометрии, где каждая фигура обладает своими оригинальными свойствами и особенностями. В данном случае речь идет о эллипсе – замечательной кривой, которая имеет некоторые созвучия со сферой, но при этом обладает своим уникальным обликом.
Сегодня мы будем исследовать эллипс с новой стороны, приблизившись к его объему через использование интеграла – мощного инструмента, позволяющего представить сложные геометрические модели в виде более простых составляющих. При помощи этого математического приема мы сможем раскрыть глубинные свойства эллипса и увидеть его внутреннюю структуру.
Эллипс, с его элегантными изгибами и симметрией, всегда притягивал внимание ученых и математиков. И сегодня, благодаря применению теории интегралов, нам предоставляется возможность посмотреть на его форму и размеры с новой стороны. Уяснение объема эллипса позволит лучше понять его внутренние пространства и логику распределения оных.
Эллипс: геометрическая фигура с уникальными свойствами
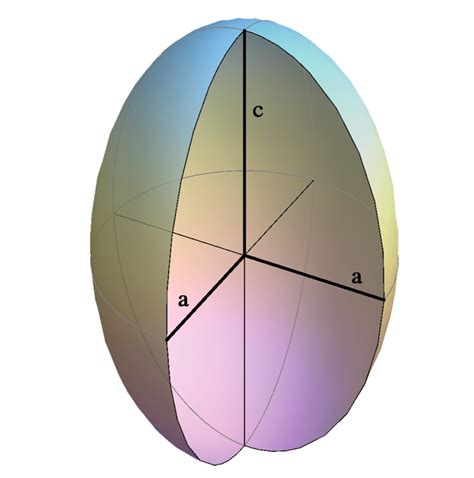
Эллипс имеет множество особенностей и применений в различных областях науки и техники. Он широко используется в астрономии для описания орбит планет и космических тел. Эллипсы можно встретить в архитектуре, дизайне, технике и во многих других областях.
Одной из ключевых характеристик эллипса является его объем. Объем эллипса - это величина, определяющая размер и пространственную вместительность данной фигуры. Вычисление объема эллипса позволяет определить его важные параметры и использовать в соответствующих задачах и приложениях.
Чтобы вычислить объем эллипса, необходимо использовать интеграл, который основывается на специальной формуле, зависящей от основных параметров фигуры.
Знание того, как вычислять объем эллипса, может быть полезно при решении различных задач, связанных с геометрией, механикой, физикой и многими другими научными и практическими областями. Используя интегралы, можно получить точные результаты, которые позволяют более глубоко изучить свойства эллипса и применять их в практике.
Таким образом, понимание сути эллипса и его объема является важным знанием для тех, кто интересуется геометрией и ее приложениями. Вычисление объема эллипса через интеграл позволяет углубиться в изучение этой структуры и использовать его результаты в решении реальных задач.
Основные аспекты определения геометрической фигуры - эллипса
На первый взгляд, эллипс может показаться простым овалом или вытянутым кругом, но на самом деле эта фигура имеет набор особенностей, которые делают ее уникальной. Определение эллипса находится на пересечении геометрии и алгебры, и может быть выражено через точки, отрезки, уравнения и параметры.
Эллипс можно рассматривать как плоскую фигуру, которая образуется при движении точки, находящейся внутри фигуры, по заданному закону. Главная характеристика эллипса - его полуоси, которые определяются длинами двух отрезков, проходящих через центр эллипса и расположенных вдоль его осей.
Эллипс также может быть описан в терминах фокусов и прямоугольников. Фокусы эллипса - это две точки внутри фигуры, сумма расстояний от которых до любой точки эллипса остается постоянной. Прямоугольник, в котором можно поместить эллипс, называется описанным прямоугольником и имеет свои особенности.
Установление этих определений и свойств эллипса является ключом к его дальнейшему изучению и применению в различных областях, включая математику, физику и инженерию. Глубокое понимание этих характеристик позволяет анализировать и определять объем эллипса с помощью математического интеграла и других специфических методов.
Геометрические параметры эллипса
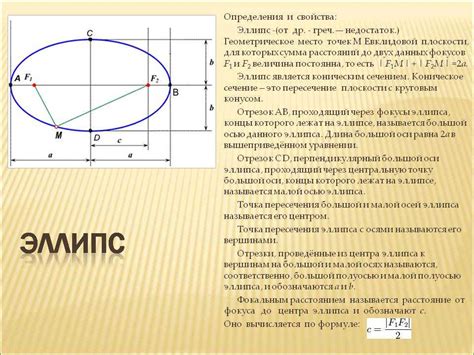
Один из основных параметров эллипса - его радиус. Однако, для эллипса также характерно наличие двух радиусов: большого радиуса (полярного радиуса) и малого радиуса (апполониевого радиуса). Большой радиус является расстоянием от центра эллипса до самой удаленной точки на его окружности, а малый радиус - половиной расстояния между фокусами эллипса.
Помимо радиусов, эллипс также характеризуется его эксцентриситетом. Эксцентриситет является мерой "сплющенности" эллипса и выражает соотношение между его большим и малым радиусами. Чем ближе эксцентриситет к нулю, тем более "круглым" является эллипс.
Еще одним параметром эллипса является его фокусное расстояние. Фокусное расстояние представляет собой расстояние между фокусами эллипса, которые являются особыми точками, относительно которых строится фигура. Фокусы эллипса играют важную роль в определении его формы.
| Параметр | Описание |
|---|---|
| Большой радиус | Расстояние от центра эллипса до самой удаленной точки на его окружности |
| Малый радиус | Половина расстояния между фокусами эллипса |
| Эксцентриситет | Мера "сплющенности" эллипса, отражающая соотношение между его радиусами |
| Фокусное расстояние | Расстояние между фокусами эллипса, определяющее его форму |
Роль интеграла в вычислении объема эллипса

В данном разделе рассмотрим методы вычисления объема эллипса с использованием интеграла. Интеграл, как важная математическая концепция, позволяет нам решать различные задачи, в том числе и определение объемов сложных геометрических форм, таких как эллипс. В основе использования интеграла лежит принцип разбиения фигуры на бесконечное число маленьких элементов, после чего их суммирование приводит к точному результату.
Один из подходов к вычислению объема эллипса заключается в использовании трехмерных интегралов и теории множества. Определенный интеграл позволяет нам выразить объем эллипса через его параметры, такие как полуоси и фокусное расстояние. Разбивая эллипс на бесконечно маленькие объемные элементы и интегрируя их с учетом соответствующих ограничений, мы получаем точный объем данной фигуры.
Другим методом вычисления объема эллипса является использование одномерного интеграла. Он представляет собой интегрирование криволинейной функции, задающей форму эллипса, по одной из переменных. Такой подход позволяет нам определить площадь поперечного сечения эллипса и далее интегрировать ее по оси, чтобы получить объем фигуры.
Описанные методы являются универсальными при вычислении объема эллипса через интеграл, так как они позволяют работать с различными типами эллипсов, в том числе и с несимметричными. Вычисление объема с использованием интеграла требует определенных математических знаний и навыков, однако оно позволяет получить точный результат без использования геометрических аппроксимаций.
Переход к полярным координатам для определения объема эллипса
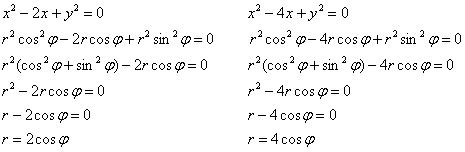
В данном разделе мы рассмотрим метод перехода к цилиндрическим (полярным) координатам для нахождения объема эллипса. Использование цилиндрических координат позволяет упростить интегральное вычисление и создать удобную систему измерения для тел с цилиндрической симметрией, таких как эллипсы и окружности.
Полярные координаты представляют собой систему координат, где точка определяется расстоянием от начала координат до точки (радиусом) и углом, который образует линия, соединяющая начало координат и точку, с положительным направлением осей координат.
Переход к цилиндрическим координатам позволяет нам выразить эллипс как функцию от радиуса и угла. В результате, объем эллипса может быть выражен через интеграл в полярных координатах.
При использовании этого метода, мы можем разбить эллипс на бесконечно малые элементы и интегрировать их объемы, чтобы найти общий объем эллипса. В процессе интегрирования, мы учитываем изменение радиуса и угла, чтобы точно описать форму эллипса.
Для проведения подобного интегрирования в цилиндрических координатах, необходимо учитывать элементарный объем в полярной системе координат, а также ограничения эллипса. Зная эти параметры, мы можем записать интеграл для нахождения объема эллипса и использовать методы вычисления интегралов для получения численного результата.
Цилиндрические координаты в эллиптической системе
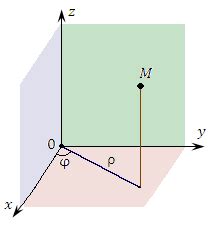
В цилиндрических координатах точка пространства задается тройкой чисел: расстоянием от точки до начала координат, углом между линией, соединяющей точку с началом координат, и некоторой фиксированной осью, а также высотой точки над некоторой фиксированной плоскостью. В эллиптической системе цилиндрические координаты применяются для описания объемов и форм эллипсоидов, что имеет большое значение в различных областях науки и техники.
Благодаря использованию цилиндрических координат в эллиптической системе становится возможным получение удобных аналитических выражений для объемов эллипсоидов. Это позволяет эффективно использовать интегральные методы для нахождения объема эллипсов. Зная аналитическую формулу для перехода от прямоугольных координат к цилиндрическим в эллиптической системе, можно свести задачу нахождения объема эллипса к вычислению определенного интеграла.
Таким образом, использование цилиндрических координат в эллиптической системе является важным инструментом для анализа и вычисления объема эллипсов. Это позволяет более наглядно и эффективно работать с данными фигурами, открывая новые возможности в области математики и приложений в реальном мире.
Вычисление интеграла в цилиндрической системе координат

В данном разделе рассмотрим способы вычисления интегралов с использованием цилиндрической системы координат. Цилиндрическая система координат представляет собой альтернативный способ описания трехмерного пространства, где вместо декартовых координат (x, y, z) используются полярная координата радиуса (ρ), азимутальный угол (φ) и высота (z).
Использование цилиндрической системы координат в вычислениях интегралов может быть удобным в определенных случаях, например, при интегрировании функций, симметричных относительно оси z или симметричных сферически относительно начала координат. Для проведения вычислений в цилиндрической системе координат необходимо заменить дифференциалы декартовых координат на дифференциалы цилиндрических координат и изменить пределы интегрирования соответствующим образом.
Одна из важных задач, которую можно решить с использованием цилиндрической системы координат, - это вычисление объема тела, ограниченного поверхностью одного или нескольких эллипсоидов. В данном разделе мы рассмотрим способы вычисления такого объема с помощью интегралов в цилиндрической системе координат. Обратите внимание, что интегралы будут написаны в соответствии с дифференциалами цилиндрических координат.
Примеры решения задач с применением метода интеграла

В каждом примере решения задачи подробно описывается процесс применения метода интеграла. Рассматривается выбор подходящих пределов интегрирования, построение соответствующих интегральных функций, а также последовательные шаги для получения окончательного результата. Представленные примеры решения задач с использованием метода интеграла помогут расширить понимание и навыки в применении этого метода к различным математическим и физическим задачам.
Примеры решения задач охватывают различные области математики и физики, включая нахождение площади фигур, вычисление объемов тел, определение центров масс и другие важные величины. Каждый пример сопровождается подробными выкладками и объяснениями, что поможет читателю лучше понять принципы и методы интеграла. Представленные примеры решения задач обладают разной сложностью, что позволяет читателю с различным уровнем подготовки углубить свои знания в области интеграла и его применения в практических задачах.
Новые горизонты в определении объема шарообразного эллипсоида

Прежде всего, необходимо отметить, что шарообразный эллипсоид является особым типом эллипсоида, обладающим сферической симметрией. Стандартные способы расчета объема не всегда могут быть применены в данном случае, поэтому требуется использование интегральных методов.
Одним из важных шагов в процессе определения объема шарообразного эллипсоида является выбор соответствующей системы координат. Применение сферической системы координат позволяет значительно упростить математические выкладки и получить удобные интегральные представления для нахождения объема.
Для точного нахождения объема шарообразного эллипсоида мы используем численные методы интегрирования, такие как метод Монте-Карло и численное интегрирование по Уортону. Эти методы позволяют вычислить объем с высокой точностью, учитывая особенности геометрии данного объекта.
Таким образом, применение интегральных методов и численных алгоритмов позволяет достичь точного значения объема шарообразного эллипсоида и расширяет нашу возможность изучения и понимания этого уникального геометрического объекта в пространстве.
Вопрос-ответ

Какой интеграл использовать для нахождения объема эллипса?
Для нахождения объема эллипса можно использовать интеграл, известный как интеграл объема. Он вычисляется по формуле V = ∫∫∫ dV, где dV - элемент объема в декартовых координатах.
Какова формула для вычисления объема эллипса через интеграл?
Формула для вычисления объема эллипса через интеграл имеет вид V = ∫∫∫ dV = ∫∫∫ dx dy dz, где интеграл берется по всей области эллипса в пространстве. В данной формуле dx, dy и dz - это изменения координат в каждом измерении.
Какие границы интегрирования следует использовать для нахождения объема эллипса через интеграл?
Для нахождения объема эллипса через интеграл необходимо определить границы интегрирования для каждой переменной. Обычно это делается путем задания интервалов, в которых находятся значения переменных x, y и z, ограничивающих область эллипса. Например, пусть эллипс задан уравнением x^2/a^2 + y^2/b^2 + z^2/c^2 = 1, то границы интегрирования будут определяться значениями переменных x, y и z, которые удовлетворяют этому уравнению.